Concepto de espontaneidad de las reacciones químicas
En la naturaleza existen multitud de reacciones químicas que son espontáneas. ¿Qué entendemos por reacción espontánea? Significa que, una vez que la reacción se inicia, transcurre por sí misma, sin un aporte energético externo, hasta que se agotan los reactivos o se agota el reactivo limitante, si lo hay. Podemos visualizar de forma sencilla la espontaneidad de un proceso si imaginamos que echamos a rodar una pelota por una pendiente: una vez que la echamos a rodar no se detendrá en mitad de la cuesta, sino que continuará en movimiento hasta llegar a una zona llana en la que pierda por rozamiento su energía cinética. Una reacción espontánea, de forma similar a la pelota, no se detendrá hasta que los reactivos se transforme por completo en productos.
Estos procesos espontáneos son, además, irreversibles, es decir, no pueden revertir sin un aporte energético externo. Los productos no se recombinan espontáneamente para dar de nuevo los reactivos, igual que la pelota, una vez en terreno llano, no comienza a subir de nuevo la pendiente por sí sola (a no ser que le demos una patada, lo cual ya supondría un aporte energético externo, es decir, un proceso no espontáneo).
Por tanto, como decimos, en la naturaleza existen multitud de procesos espontáneos: la expansión de un gas, la oxidación del hierro… Ahora bien, ¿cómo podemos saber si un proceso dado será o no espontáneo? ¿Qué criterios termodinámicos debemos utilizar? Ya hemos tratado en profundidad en los apartados de teoría previos el concepto de entalpía y lo que son las reacciones endotérmicas y exotérmicas.
![Diagrama de entalpía para una reacción exotérmica Diagrama de entalpía para una reacción exotérmica, es decir, con entalpía negativa]()
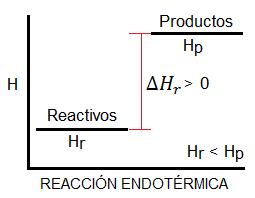
![Diagrama de entalpía para una reacción endotérmica Diagrama de entalpía para una reacción endotérmica, es decir, con entalpía positiva]()
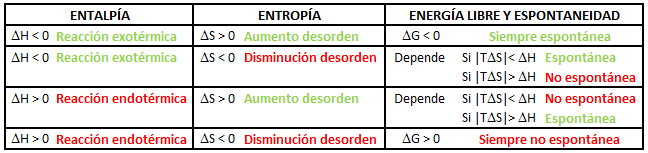
Podríamos pensar que una reacción exotérmica, que desprende calor al entorno, siempre será espontánea, dado que los sistemas tienden a un mínimo de energía, y en las reacciones exotérmicas los productos tienen menos energía que los reactivos (tal y como vemos en el diagrama). Es cierto que muchas reacciones espontáneas son exotérmicas y que la mayoría de reacciones exotérmicas son espontáneas; sin embargo, esto no es siempre así. Existen reacciones exotérmicas que no son espontáneas a ciertas temperaturas, y reacciones endotérmicas que sí lo son.
Por tanto, el criterio energético, es decir, el signo de la variación de entalpía ΔH, no es suficiente por sí mismo para decidir si un proceso será o no espontáneo, ya que en verdad, si consideramos el conjunto sistema-entorno, la energía siempre se conserva.
El concepto de entropía: el grado de desorden de los sistemas químicos
Así, para determinar la espontaneidad o no espontaneidad de una reacción química, se hace necesario introducir una variable termodinámica de la cual no habíamos hablado hasta el momento, que es la entropía, representada con una letra S mayúscula. La entropía es una función de estado (depende únicamente de los estados inicial y final) extensiva (depende de la cantidad de materia total), cuyas unidades son generalmente J/K·mol. De forma simplificada, podemos definir la entropía como una medida del desorden microscópico de un sistema. Así, la variación de entropía global para un sistema, será:
ΔS = Sfinal – Sinicial
Y tenemos que:
ΔS > 0 Aumento del desorden
ΔS < 0 Disminución del desorden
Un sistema muy desordenado tiene una elevada entropía, mientras que un sistema muy ordenado tiene una baja entropía. Por ejemplo, si consideramos los tres estados de agregación del agua, sus entropías serán:
Shielo = 44,8 J/K·mol < Slíquido= 69,9 J/K·mol < Svapor= 188,8 J/K·mol
En general:
Ssólido< Slíquido< Sgas
En un sistema aislado y a volumen constante (que no puede intercambiar ni materia ni energía con el entorno) se dará espontáneamente aquel proceso en el que se produzca un aumento de la entropía, esto es, aquel proceso en el que aumente el desorden. Es decir, en general, los sistemas tienden a un aumento del desorden. Es por este motivo que existen reacciones endotérmicas que son espontáneas; reacciones que por criterios energéticos pareciera que no deben producirse espontáneamente y que, sin embargo, sí ocurren de este modo, porque en el transcurso de las mismas la entropía aumenta considerablemente.
En los próximos apartados profundizaremos un poco más en el concepto de entropía y en la espontaneidad de las reacciones químicas:
Termodinámica Teoría 17: Segundo Principio de la Termodinámica. Entropía del Universo.
Termodinámica Teoría 18: Tercer Principio de la Termodinámica. Concepto de entropía molar estándar.
Termodinámica Teoría 19: ¿Cómo calcular la variación de entropía de una reacción a partir de las entropías molares estándar?