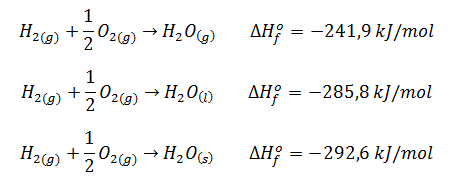En este ejercicio de enlace químico debemos asignar una serie de valores de puntos de fusión a ciertos compuestos. El enunciado es:

Asigne los puntos de fusión siguientes: 3550ºC, 650ºC, -107ºC y -196ºC a los compuestos: nitrógeno, aluminio, diamante y tricloruro de boro; justifique el tipo de enlaces o fuerzas intermoleculares que presenta cada uno de estos compuestos en estado sólido.

Para ello debemos recordar que los compuestos con mayor punto de fusión de la naturaleza son las redes covalentes (como el diamante) y, tras ellos, de forma general, las redes metálicas (como el aluminio), mientras que las sustancias que presentan únicamente fuerzas intermoleculares de dispersión o de London son las sustancias con menores puntos de fusión existentes (como el nitrógeno y el tricloruro de boro).

También te puede interesar:

Justificar los puntos de ebullición del etano, dimetiléter y etanol

Puntos de ebullición de los compuestos de hidrógeno de halógenos y anfígenos

Ordenar por puntos de ebullición etanol, butano, agua y metano

En este apartado comenzamos el tema de Termoquímica o Termodinámica Química, términos con los que en este curso haremos referencia indistinta al estudio de las transferencias energéticas aplicado a las reacciones químicas.

En todo proceso, tanto físico como químico, están implicadas ciertas energías de distintos tipos (energía potencial, energía cinética, energía eléctrica…). La ciencia que estudia los cambios energéticos en sus distintas manifestaciones, en cualquier tipo de proceso, recibe el nombre de termodinámica. Si dicha ciencia se aplica al estudio de los cambios químicos, entonces, como hemos comentado previamente, la llamaremos termoquímica o termodinámica química. Aunque en ocasiones no se consideran términos equivalentes, en este curso no haremos distinción entre ellos.

Este estudio energético de los cambios químicos es fundamental para tener una visión completa de las reacciones químicas, ya que estas obedecen a dos leyes fundamentales:

• La Ley de Conservación de la Masa (Ley de Lavoisier). Durante una reacción química no se crea ni se destruye materia, la masa de reactivos inicial es igual a la masa final de productos.
• La Ley de Conservación de la Energía, que constituye el Primer Principio de la Termodinámica en su formulación más simple, que es que “la energía ni se crea ni se destruye, sólo se transforma”. En un apartado posterior tratamos en profundidad este Primer Principio.

La segunda ley, relativa a la energía, es también importante dado que todo proceso químico lleva siempre asociadas variaciones energéticas entre reactivos y productos. La energía de estos cambios puede ser de distintos tipos: energía luminosa, energía eléctrica, trabajo mecánico… aunque lo más habitual es que se manifieste como un flujo de calor entre el sistema reaccionante y el entorno.

Vemos que han surgido dos conceptos, el de sistema y entorno, que surgen de la necesidad de delimitar el objeto de estudio para poder estudiar los cambios de energía asociados a una reacción química. El SISTEMA es la parte del Universo que se aísla del resto para observarlo, en nuestro caso, por ejemplo, un recipiente en el que tiene lugar una reacción química, o un proceso físico relacionado con una sustancia, como una disolución, una fusión, una vaporización…; el ENTORNO es todo lo que rodea al sistema, pudiendo estar relacionado con el mismo o no estarlo.

 

La separación entre el sistema y el entorno puede ser real o imaginaria. Por ejemplo, puede ser física, como las paredes de un tubo de ensayo, de un erlenmeyer o de un vaso de precipitados, o una delimitación imaginaria establecida de un modo arbitrario, como una zona de la atmósfera en torno a una hoguera con la cual deseamos estudiar una reacción de combustión:

Los sistemas termodinámicos se clasifican en sistemas abiertos, cerrados o aislados según su capacidad para intercambiar materia y energía con el entorno. Así:

• Sistema abierto: puede intercambiar con el entorno tanto materia como energía, generalmente en forma de calor. Por ejemplo, la combustión de madera al aire libre, o una reacción química en un vaso de laboratorio abierto, que permite tanto el paso de calor a través de las paredes del recipiente (se dice que el recipiente tiene paredes diatérmicas) como desprendimiento de gases.
• Sistema cerrado: puede intercambiar energía con el entorno, pero no materia. Por ejemplo, un recipiente cerrado de vidrio en el que se lleva a cabo una reacción química que desprende calor. Los gases formados no pueden abandonar dicho recipiente porque está cerrado con un tapón, pero el calor sí que puede desprenderse porque las paredes de vidrio son diatérmicas. Si tocamos el recipiente con las manos, lo notaremos caliente.
• Sistema asilado: no es posible el intercambio ni de materia ni de energía. Por ejemplo, lo que se conoce coloquialmente como un termo, que técnicamente es un vaso Dewar y que se usa para llevar infusiones o café y que se mantengan calientes más tiempo, es en teoría un sistema aislado, que no permite ni el paso de materia ni de energía. No obstante, los sistemas aislados son teóricos, en la práctica siempre hay cierto intercambio leve de energía y al final, el café se acaba enfriando (¡mala suerte!).

Calorímetro de laboratorio: ejemplo de sistema aislado

Asimismo, los sistemas reaccionantes también se pueden clasificar en función del estado de agregación de reactivos y productos. Si todos los componentes se halla en el mismo estado de agregación (sólido, líquido o gas), es decir, tenemos una sola fase, tendremos lo que se denomina un sistema homogéneo. Por ejemplo, la combustión del metano es un sistema homogéneo, ya que todos los componentes son gases:

Si tenemos componentes con distintos estados de agregación, es decir, tenemos varias fases, entonces se trata de un sistema heterogéneo. Por ejemplo, la descomposición de carbonato de magnesio sólido por calcinación con desprendimiento de dióxido de carbono:

Especificados ya los tipos de sistemas termodinámicos que existen, en el Apartado 2 de teoría de Termoquímica nos centraremos en el estudio de las llamadas variables termodinámicas.

En esta página hallarás todos los apartados relativos a la teoría de Termodinámica Química o Termoquímica, términos que a lo largo de este curso usaremos de forma indistinta. Puesto que tiene estructura de libro, el tema se desarrolla con un orden perfectamente establecido, tocando todos los conceptos teóricos necesarios para dominar la materia (sistemas termodinámicos, variables termodinámicas, funciones de estado, transferencia de energía en forma de calor o de trabajo, primer principio de la termodinámica, energía interna, entalpía, entropía…) por lo que te recomendamos que veas los vídeos en el orden propuesto y que resuelvas tus dudas antes de continuar avanzando.

Termoquímica Teoría 1: Introducción a la termodinámica química. Sistemas termodinámicos.

Hemos visto en el primer apartado de introducción a la termodinámica química el concepto de sistema y los tipos de sistemas termodinámicos existentes. Ahora bien, una vez delimitado un sistema termodinámico, ¿qué necesitamos conocer para definirlo en profundidad? Necesitamos conocer, además de la composición química del sistema, el valor de una serie de variables que determinan el estado del mismo desde un punto de vista macroscópico. A estas variables se las denomina Variables Termodinámicas. Algunos ejemplos de Variables Termodinámicas son: volumen, temperatura, presión…

Dichas variables se clasifican en dos tipos, atendiendo a su dependencia o independencia con la cantidad total de materia presente en el sistema. Así, tenemos:

• Variables extensivas: si su valor depende de la cantidad o porción de sistema que se considera, por ejemplo: masa, volumen, número de moles…
• Variables intensivas: si su valor no depende de la cantidad de sistema considerado, por ejemplo: temperatura, densidad, presión, concentración…

Una forma sencilla de distinguir si una variable es extensiva o intensiva es dividir el sistema en dos bloques iguales y considerar si dicha variable cambia o se mantiene constante con respecto al sistema completo. Imaginemos que tenemos el siguiente sistema, constituido por 1 mol de hidrógeno en un recipiente de 22,4 litros:

Aunque para el sistema anterior hemos indicado muchas variables, para describir por completo el estado de un sistema no es necesario conocerlas todas, se pueden limitar, dado que las variables termodinámicas se hallan relacionadas entre sí por ecuaciones matemáticas. Por ejemplo, la ecuación de Clapeyron para los gases ideales:

P·V = n·R·T

Donde:

P = presión (atm o pascales, Pa)

V = volumen (litros o m3)

n = número de moles

R = constante de los gases ideales, 0,082 atm·l/K·mol o 8,31 J/K·mol

T = temperatura en grados kelvin (K)

Dada esta ecuación para los gases ideales, bastará conocer la presión, el volumen y la temperatura para definir el estado del sistema, y el número de moles, o la densidad, o la masa, se podrían calcular conociendo dichos valores de P, V y T. Por tanto, con estas variables el sistema quedaría totalmente descrito.

De este modo, un procedimiento habitual a nivel experimental para facilitar el estudio de los sistemas termodinámicos es limitar el número de variables de dicho sistema, manteniendo algunas fijas. Por ejemplo, si estudiamos un proceso a una temperatura constante de 25ºC, la temperatura dejará de ser una variable (no varía) y pasará a ser un valor numérico. Este tipo de proceso en el que se fija una variable adopta su nombre en función de cuál sea la variable fijada:

• A los procesos que se llevan a cabo a temperatura constante, se los denomina isotermos o isotérmicos (T = cte)
• A los procesos que se llevan a cabo a presión constante, se los denomina isobáricos (P = cte)
• A los procesos que se llevan a cabo a volumen constante, se los denomina isocoros (V = cte)
• A los procesos que se llevan a cabo sin transferencia de calor entre el sistema y el entorno, se los llama adiabáticos (Q = 0)

Por último, aunque no por ello menos importante, debemos saber que algunas variables termodinámicas son, además, lo que se conoce como funciones de estado. ¿Qué significa esto? Significa que si el sistema sufre una modificación y pasa de un estado A a un estado B, el valor de estas variables termodinámicas que son funciones de estado no depende de cómo se ha efectuado la transformación, sólo del estado del sistema.

Veremos esto con un ejemplo concreto para que sea más sencillo, tomando como variable la temperatura. Consideremos un sistema que está en un estado A en el cual la temperatura es de 20ºC. Este sistema sufre una transformación y pasa a estar en un estado B en el cual la temperatura es de 60ºC. El sistema en le estado B seguirá estando a 60ºC independientemente del camino que haya seguido la transformación. No depende del camino que ha seguido dicha transformación, no importa si se ha calentado y luego enfriado, o si se ha calentado progresivamente… La temperatura en el estado B seguirá siendo de 60ºC, sin importar cómo se ha llegado a ello. Por esto, la temperatura es una función de estado, sólo depende del estado del sistema en el momento en que lo consideremos.

Otra forma de decir esto es que las variaciones que experimentan las funciones de estado sólo dependen del estado inicial y final del sistema. En nuestro caso la variación de temperatura es de 40ºC (60 – 20).

Otras variables termodinámicas que son función de estado son el volumen, la presión, y otros nuevos conceptos en los que vamos a profundizar a lo largo del tema como la energía interna, la entalpía, la entropía y la energía libre de Gibbs.

Aunque en la mayor parte del tema de termoquímica vamos a considerar las transferencias o variaciones de energía calorífica de una reacción química, en este apartado vamos a hablar de otro modo distinto de variación de energía, que es el trabajo mecánico de cambio de volumen (expansión o compresión) de un gas, ya que este concepto volverá a aparecer cuando hablemos del Primer Principio de la Termodinámica (apartado 5), que es parte esencial de este tema.

¿Qué es el trabajo de compresión o expansión de un gas?

El trabajo de cambio de volumen de un gas es el trabajo necesario para que el gas pase de un volumen inicial Vi a un volumen final Vf. Si el volumen disminuye, el gas se habrá comprimido y hablaremos de trabajo de compresión; si el volumen aumenta, el gas se habrá expandido y hablaremos de trabajo de expansión.

Para ilustrar mejor este trabajo de expansión o compresión de un gas, imaginemos un gas cerrado dentro de un recipiente, una de cuyas paredes es un émbolo móvil (como el de una jeringa) pero sin masa ni rozamiento. Si se produce una variación del volumen del recipiente, el émbolo se desplazará una distancia Δx, ya que en su expansión el gas empuja el pistón contra la presión externa, que permanece constante.

Puesto que el trabajo es es fuerza por desplazamiento, podemos escribir que:

W = -Fext·Δx

Y la fuerza es presión·superficie: Fext = P·S

W = -P·S·Δx

Mientras que la superficie por la variación de x que sufre el émbolo es la variación de volumen que experimenta el recipiente:

S·Δx = ΔV

De modo que finalmente el trabajo de expansión es:

Criterio de signos en el trabajo de compresión y expansión de un gas

Si aumenta el volumen, es el gas, es decir, el sistema, el que realiza un trabajo mecánico. Según el criterio de signo que adoptaremos, que es el establecido por la IUPAC, este trabajo realizado por el sistema se considera de signo negativo, es decir, W < 0.

Si disminuye el volumen, es el entorno el que ejerce un trabajo sobre el sistema, en cuyo caso, según el criterio de signos establecido por la IUPAC, consideraremos que le trabajo es positivo, W > 0.

NOTA: Es posible que en algunos textos se halle un criterio de signos distinto a este para el trabajo, considerándose que W = +P·ΔV y que por tanto W > 0 para el trabajo realizado por el sistema y W < 0 para le trabajo realizado sobre el sistema. Esto es habitual en tratados de física y de ingenierías, aunque para Química lo más habitual es considerar el criterio de signos expuesto aquí, que es el establecido por la IUPAC.

Ejemplo numérico simple de cálculo del trabajo de expansión de un gas

A continuación vamos a realizar un ejercicio numérico muy sencillo sobre le trabajo de expansión de un gas. El enunciado es:

Un gas se expande de un volumen inicial de 4 litros a un volumen de 9 litros, contra una presión externa constante de 2 atmósferas. Calcular el trabajo realizado por el sistema.

Como hemos dicho en el primer apartado introductorio sobre termoquímica los procesos químicos y físicos de las sustancias llevan asociados cambios o variaciones de energía, y la forma de energía más habitual de dichas variaciones es como calor o energía calorífica. El intercambio de calor entre un sistema y su entorno se produce como consecuencia de una diferencia de temperatura, por ejemplo:

Siempre se produce un flujo de calor desde el elemento de mayor temperatura al de menor temperatura. En concreto, la transferencia de calor, Q, que experimenta un sistema formado por una sustancia pura depende de:

• La variación de temperatura que experimenta, ΔT
• La masa de la sustancia, m
• La naturaleza de la sustancia. De dicha naturaleza dependen dos parámetros que vamos a definir a continuación, la capacidad calorífica específica y la capacidad calorífica molar.

Capacidad calorífica específica o calor específico de una sustancia

La capacidad calorífica, c, o calor específico, es la energía calorífica necesaria para aumentar 1ºC o 1K (si hablamos de incrementos es lo mismo) la temperatura de 1kg de masa de una sustancia a una presión de 1013 hPa, En el SI se expresa en J/kg·K y es una propiedad característica de las sustancias.

Esto significa que para que un kg de agua aumente 1ºC su temperatura a presión normal, se han de suministrar 4180 J de energía calorífica.

En general, conociendo la masa de sustancia, m, la variación de temperatura que experimenta, ΔT, y su capacidad calorífica específica se puede calcular la energía calorífica intercambiada o transferencia de calor, Q, según la fórmula:

Q=m·c·ΔT

Donde:

m = masa de la sustancia

c = capacidad calorífica específica

ΔT = T_f – T_i  (temperatura final menos temperatura inicial del sistema)

Por ejemplo, para calentar una barra de 6kg de aluminio de 25ºC a 40ºC, sabiendo que la C del aluminio es de 895 J/kg·K 

Q = m·c·ΔT = 6 kg · 895 (J/K·Kg) · (40-25) = 80550 J

Capacidad calorífica molar de una sustancia

La Capacidad calorífica molar, Cm, es la energía calorífica necesaria para aumentar 1K o 1ºC la temperatura de un mol de cualquier sustancia. En este caso, la transferencia de calor será:

Q= n·ΔT·Cm

Donde:

n = número de moles

Cm = capacidad calorífica molar

ΔT = T_f - T_i  (temperatura final menos temperatura inicial del sistema)

Cabe destacar que para el caso de sólidos y líquidos, la capacidad calorífica específica y la capacidad calorífica molar son iguales si el proceso se realiza a presión constante como se se realiza a volumen constante. No obstante, en el caso de los gases, estos parámetros varían, lo cual se indica con un subíndice v y p para el proceso a V=cte y P=cte respectivamente: Cv, Cp, Cmv, Cmp, por lo que si en un ejercicio debemos calcular el calor transferido en el caso de un gas nos deben indicar si el proceso es isocoro o isobárico.

Hemos visto en el primer apartado introductorio sobre termoquímica, que toda reacción química obedece a dos leyes fundamentales, la Ley de conservación de la masa y la Ley de conservación de la energía. Es esta segunda, la Ley de Conservación de la Energía, la que constituye o surge del Primer Principio de la Termodinámica o Primera Ley de la Termodinámica. Este Primer Principio establece, por tanto, que la energía siempre se conserva, de modo que si en un sistema capaz de intercambiar energía, la energía disminuye, necesariamente aparecerá una cantidad de energía equivalente en el entorno, ya que la energía no se crea ni se destruye, sólo se transforma.

Matemáticamente, el Primer Principio de la Termodinámica determina cómo afectan los intercambios de calor, Q, y trabajo, W, a la energía global de un sistema. Es por este motivo que la transferencia de energía en forma de calor y la transferencia de energía en forma de trabajo las hemos tratado en dos apartados previos de teoría.

Así, la ecuación matemática del Primer Principio es:

Siendo, según el criterio de signos establecido por la IUPAC, y explicado en el apartado 3, positivo el calor y el trabajo que entra o se realiza sobre el sistema, y negativo el calor que sale del sistema o el trabajo realizado por el mismo.

U es una función de estado que introducimos por primera vez en este tema y que recibe el nombre de energía interna del sistema. Así, se puede enunciar la Primera Ley de la Termodinámica como:

La variación de energía interna de un sistema es igual a la suma del calor y el trabajo que intercambia con su entorno.

Pero… ¿qué es la energía interna de un sistema? Es la energía asociada a la estructura interna del sistema, es decir, la suma de todas las energías contenidas en el mismo, como la energía cinética de sus partículas individuales (núcleos, átomos, moléculas… que pueden vibrar, rotar o incluso efectuar movimientos de traslación, como los gases) y la energía potencial de éstas, esencialmente energía potencial eléctrica debida a atracciones núcleo-electrón, repulsiones núcleo-núcleo y repulsiones electrón-electrón.

El valor absoluto de la energía interna de un sistema, U, se desconoce por su gran complejidad, pero sí que podemos medir o determinar su variación, ΔU, cuando pasa de un estado inicial a un estado final, ya que, como hemos dicho, la energía interna es una función de estado y sólo depende de dichos estados inicial y final:

En cuanto a la aplicación del Primer Principio de la Termodinámica a las reacciones químicas, que es lo que nos interesa en este caso, la variación de energía interna representa la diferencia de energía entre los productos y los reactivos, siendo Q y W la transferencia de calor como calor y como trabajo que acompañan a dicha reacción química.

En concreto, en este curso vamos a aplicar el Primer Principio de la Termodinámica a las reacciones químicas en dos casos particulares, cuando el volumen permanece constante, es decir, es un proceso isocoro, y cuando la presión permanece constante, es un proceso isobárico. Este último caso, la reacción química a presión constante, es de suma importancia, ya que de aquí surge el concepto de Entalpía, el cual se va a desarrollar con muchísima amplitud a lo largo del tema.

A continuación, en los dos siguientes apartados, vamos a estudiar para una reacción la transferencia de calor a volumen constante y la transferencia de calor a presión constante.

Existen algunas reacciones química que transcurren a volumen constante, es decir, sin variación apreciable en el volumen total del sistema. Son ejemplos de ello las reacciones que se dan entre sólidos y líquidos sin desprendimiento de gases, ya que en estos la variación es muy pequeña y se puede despreciar, o también las que se llevan a cabo en un recipiente cerrado, como un termo o un calorímetro, aunque intervengan gases. Son ejemplos de esto la comida cocinada en la olla a presión, la esterilización del material de laboratorio en un autoclave o la fermentación del vino en un recipiente cerrado para convertirse en cava.

Veamos cómo aplicar el Primer Principio de la Termodinámica a estos procesos. Recordemos que matemáticamente, se expresa como:

y que hemos deducido en el tercer apartado

De modo que: 

Pero como no hay variación de volumen  ΔV = 0, y por tanto el producto  - PΔV también será 0 y quedará :

 Como el proceso es a volumen constante, éste será el calor transmitido a volumen constante  lo cual se indica añadiendo v subíndice.

Por tanto:

El calor absorbido o desprendido en una reacción química realizada a volumen constante, Q_v, es igual a la variación de energía interna del sistema.

En esta apartado aplicaremos nuevamente el Primer Principio de la Termodinámica a un tipo concreto de reacciones química, en este caso, a las que transcurren a presión constante, que son las más habituales. Aunque hemos visto algunas reacciones que transcurren a volumen constante en el apartado 6, la mayor parte de reacciones químicas suceden a presión atmosférica y con variación de volumen, ya que se llevan a cabo al aire libre. Por ejemplo, una hoguera o en recipientes abiertos en el laboratorio: un vaso de precipitados, un enlermeyer…

Cuando aplicamos el Primer Principio de la Termodinámica a estas reacciones, surge una nueva función de estado, denominada entalpía que es un concepto fundamental en termoquímica. Veremos a continuación cómo aplicar dicho principio a estas reacciones paso a paso hasta llegar a la deducción de la entalpía y a su relación con la variación de energía interna en una reacción química a presión constante.

La expresión matemática del primer principio es:

En este caso, dado que es una reacción que no se lleva a cabo en un recipiente cerrado, consideraremos que sí que hay una variación de volumen apreciable que será:

ΔV = Volumen productos (VP) – Volumen reactivos (VR)

Como estamos considerando la transferencia de calor a presión constante, esto se indica con una p subíndice, es decir:

 ΔU = QP - PΔV

Si despejamos este QP, pasando el término – PΔV  al otro lado sumando quedará:

QP = ΔU + PΔV

Y como ΔV =  VP - VR, 

y ΔU = UP - UR, entonces:

QP = UP - UR + P(VR - VP)

QP = UP - UR + PVP - PVR

Ahora agrupamos los términos referidos a productos y los referidos a reactivos. Queda:

QP = UP + P VP - (UR + PVR)

El producto PV tiene unidades de energía, que sumada a la energía interior U, nos da una nueva medida de energía que llamamos ENTALPÍA, representada por H, y que es una función de estado (depende de los estados final e inicial del sistema):

H = U + PV

QP = UP + PVP - (UR + PVR)

HP = UP + PVP

HR = (UR + PVR)

QP = UP+ PVP - (UR +PVR)

QP = ΔH

Como vemos, el calor absorbido o desprendido en una reacción química realizada a presión constante es igual a la variación de entalpía del sistema, siendo H, por tanto, otra forma más de medir la energía de un sistema.

Dado que la entalpía es una función de estado, como ocurre con la energía interna, U, no se puede conocer su valor absoluto, únicamente se puede medir su variación durante una reacción química.

Hemos visto en los apartados previos, el 6 y el 7, la aplicación del Primer Principio de la Termodinámica a las reacciones que transcurren a volumen constante, en cuyo caso la transferencia de calor recibe el nombre de Qv, y a las reacciones que transcurren a presión constante, que da lugar a QP. Asimismo, hemos deducido que:

ΔU = QV  y  ΔH = QP

A partir de esto podemos deducir la relación entre la variación de entalpía y la variación de energía interna.

• Relación entre QP y QV para sólidos y líquidos

En el caso de las reacciones en las que sólo intervienen sólidos o líquidos, podemos considerar que la variación de volumen entre reactivos y productos es muy pequeña y que el producto  PΔV es despreciable. Así se obtiene

QP = QV, o también, ΔH = ΔU

• Relación entre QP y QV para gases

En cambio, si en las reacciones intervienen especies gaseosas, que haya o no variación de volumen dependerá de la variación del número de moles de especies gaseosas enre reactivos y productos:

PV = nRT
PΔV = ΔnRT

Utilizamos la ecuación ya conocida QP = ΔU + PΔV y sustituiremos PΔV por ΔnRT y obtenedremos:

La variación de volumen dependerá de la variación del número de moles, ya que a más cantidad de moles gaseosos, manteniendo la presión constante, será mayor volumen.

Sólo si ΔH = 0, entonces QP = QV, sino QP ≠ QV

Para calcular Δn en una reacción vamos a ver un ejemplo concreto, consideremos la reacción de combustión del metano:

La variación del número de moles corresponde a la suma de los coeficientes estequiométricos de los productos menos la suma de los coeficientes estequiométricos de los reactivos, es decir:

Concepto de entalpía de reacción estándar: condiciones termoquímicas estándar

Vamos a profundizar en este apartado en un concepto fundamental en termoquímica, el concepto de entalpía de reacción, ΔHr. Definimos la entalpía de una reacción química como el calor absorbido o desprendido en dicha reacción química cuando ésta transcurre a presión constante, es decir:

 ΔH = QP

 ΔH : entalpía de la reacción

 QP : calor transferido a presión constante

El valor de entalpía es distinto según a qué presión y a qué temperatura se lleve a cabo la reacción. Por este motivo se definen unas condiciones estándar. Las condiciones estándar termoquímicas son 25ºC (o 298 K) y 1atm de presión (1,013·10^5 Pa). Cuando la reacción se lleva a cabo en dichas condiciones estándar, su variación de entalpía (ΔH) recibe el nombre de entalpía estándar de reacción o también entalpía normal de reacción, y se representa como ΔHor.

Las unidades de la entalpía estándar de reacción son kJ o kJ/mol, siendo esta última la forma más habitual de hallar los valores de entalpías en las distintas tablas.

Ecuaciones termoquímicas

La forma más habitual de indicar la entalpía estándar de una reacción química es en las llamadas ecuaciones termoquímicas, que consisten en escribir la reacción, correctamente ajustada y con los estados de agregación de todos los compuestos que intervienen, y añadir, a la derecha, el valor de la entalpía estándar. Por ejemplo, a continuación vemos la ecuación termoquímica para la reacción de combustión del etanol y para la reacción de combustión del monóxido de carbono:

El motivo de que en la ecuación termoquímica se deban indicar los estados de agregación de productos y reactivos, es decir, si son gases, líquidos o sólidos, y también la forma alotrópica (por ejemplo, carbono grafito o carbono diamante), es porque de ello también depende el valor de la entalpía de la reacción.

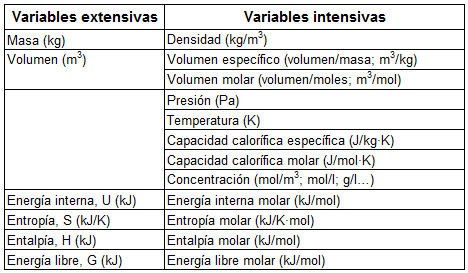
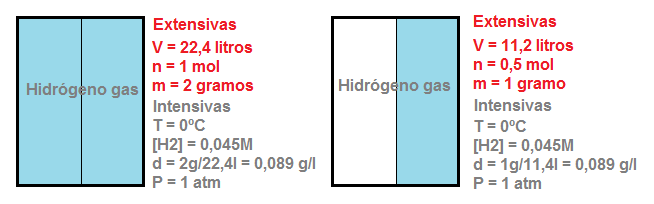
Además, puesto que la entalpía es una variable extensiva, es decir, depende de la cantidad total de materia, si la ecuación termoquímica se ajusta de un modo distinto, cambiará su valor, siempre y cuando el valor venga dado en kJ (y no en kJ/mol). Por ejemplo:

Esta ecuación termoquímica nos indica que cuando 2 moles de monóxido de carbono reaccionan con un mol de O2, se desprenden 566 kJ de calor, mientras que, tal y como hemos visto previamente en la misma reacción pero ajustada para 1 mol, se desprenden la mitad, 283 kJ de energía calorífica.

Reacciones endotérmicas y reacciones exotérmicas

En las ecuaciones termoquímicas indicadas previamente aparecen los correspondientes valores de entalpía estándar de reacción para diversas reacciones, y todas ellas tienen signo negativo. ¿Qué significa el signo de la entalpía? Según el criterio establecido por la IUPAC, que hemos explicado al hablar de la transferencia de energía en forma de calor, es negativo el calor desprendido por el sistema, y positivo el calor absorbido por el sistema. Así, si la entalpía de reacción es negativa, significa que durante el transcurso de la reacción, el sistema pierde o libera calor hacia el entorno, mientras que si la entalpía de reacción es positiva significa que durante el transcurso de la reacción, el sistema absorbe calor del entorno. En función del signo de la entalpía, las reacciones se clasifican como endotérmicas y exotérmicas:

• Una reacción exotérmica es aquella cuyo valor de entalpía es negativo, es decir, el sistema desprende o libera calor al entorno (ΔH < 0).
• Una reacción endotérmica es aquella cuyo valor de entalpía es positivo, es decir, el sistema absorbe calor del entorno (ΔH > 0).

Por ejemplo, la reacción que hemos considerado previamente, de oxidación del monóxido de carbono para dar dióxido de carbono, tiene variación de entalpía negativa:

Esto significa que se desprende calor en el transcurso de la misma y es, por tanto, una reacción exotérmica, mientras que si consideramos la misma reacción pero en sentido contrario, el valor absoluto de la entalpía se mantiene, pero el signo cambia, siendo en este caso la entalpía positiva y, por tanto, una reacción endotérmica:

Distintos tipos de entalpías de reacción: entalpías de combustión y entalpías de formación.

Aunque cualquier entalpía es, por definición, una entalpía de reacción (variación de calor a presión constante asociada a una reacción química) es frecuente especificar un poco más y, en lugar de llamarla entalpía de reacción, indicamos el tipo de reacción a que se refiere, por ejemplo, en el caso del CO y el oxígeno, se trata de una reacción de combustión, por lo que a su entalpía de reacción se la puede llamar entalpía de combustión, ΔHoc 

Del mismo modo sucede, por ejemplo, con las entalpías de las reacciones de formación de un compuesto, que reciben el nombre de entalpías de formación, y que veremos con detenimiento en el apartado próximo por su gran utilidad y la frecuencia de su uso.

Diagramas de entalpía

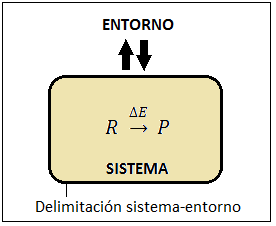
Un diagrama de entalpía es un gráfico que permite mostrar de un modo visual la variación de entalpía de una reacción química. Si nosotros tenemos una reacción:

R –> P      ΔHoR

Como el valor absoluto de entalpía no se conoce, el origen de la escala de entalpías es arbitrario. Por ello, lo que se hace es representar reactivos y productos, siendo la diferencia entre ellos el valor de entalpía de la reacción.

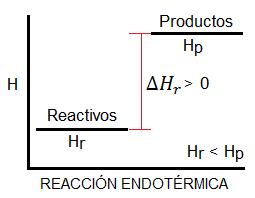
Si la reacción es endotérmica, es decir, absorbe calor, el diagrama de entalpía tendrá la forma siguiente:

Si la reacción es exotérmica, es decir, desprende calor, el diagrama de entalpía tendrá la forma siguiente:

La entalpía de formación es un tipo concreto de entalpía de reacción, que recibe el nombre de entalpía de formación estándar o entalpía normal de formación si la reacción se lleva a cabo a 25ºC y a 1 atm, que son las condiciones estándar en termoquímica. Así, la entalpía normal o estándar de formación (también llamada a veces calor normal de formación), se representa por ΔHof y es la variación de entalpía cuando se forma un mol de compuesto a partir de sus elementos en estado normal (esto es, en el estado de agregación y forma alotrópica más estable a la que dichos elemento se hallan en condiciones estándar).

Esta entalpía de formación podrá ser positiva, reacción endotérmica, o negativa, reacción exotérmica. Por ejemplo, es exotérmica la reacción de formación de peróxido de hidrógeno a partir de sus elementos, hidrógeno y oxígeno, en estado gaseoso, que es como se encuentran en condiciones estándar:

Mientras que la reacción de formación del eteno, C2H4, es endotérmica, es decir, absorbe calor cuando se produce:

Como vemos, en esta última reacción hemos indicado que el carbono, además de estar en estado sólido, está en forma de grafito. Esto se debe a que el carbono tiene distintas formas alotrópicas, es decir, compuestas por el mismo elemento pero con distintas estructuras, como el grafito y el diamante, pero la más estable a 25ºC y a 1 atmósfera de presión es el grafito, y por este motivo es esta la forma que debemos escoger para plantear las reacciones de formación en las que intervenga el carbono. Esta presentación de formas alotrópicas ocurre también en otros elementos, como el azufre, que puede presentar estructura monoclínica y rómbica, o el fósforo, que puede tener la llama estructura de fósforo blanco y la de fósforo rojo.

Asimismo, la entalpía de formación cambia si el compuesto formado está en distinto estado de agregación, aunque se parta de los mismos elementos. Por ejemplo, la entalpía de formación del agua vapor, del agua líquida y del agua sólida difieren:

No obstante, lo habitual es plantear que se produce agua líquida si estamos en condiciones estándar, ya que es así como el agua se encuentra a 25ºC y 1 atmósfera de presión.

Cabe destacar, además, que la entalpía de formación de los elementos puros se toman como 0, pues como no podemos conocer los valores absolutos de entalpía, se toman estos como referencias arbitrarias. Así, por ejemplo:

ΔHof O2(g) = 0 kJ/mol
ΔHof Cl2(g) = 0 kJ/mol
ΔHof Na(s) = 0 kJ/mol

A continuación se muestra una tabla con los valores de entalpía de formación estándar de distintos compuestos, en kJ/mol, y con sus correspondientes estados de agregación.

Clicando sobre ella puedes descargarla como imagen, y en el enlace inferior puedes descargarla como PDF.

Tabla de valores de entalpías de formación estándar de diversos compuestos en PDF

A partir de las entalpías de formación de los distintos compuestos que intervienen en una reacción química es posible calcular la entalpía o variación de entalpía de dicha reacción. Consideremos la reacción global de un reactivo A con un reactivo B, para dar un producto C y un producto D.

La variación de entalpía de esta reacción, por ser una función de estado, será la entalpía del estado final menos la entalpía del estado inicial, es decir, la entalpía de formación de los productos menos la entalpía de formación de los reactivos. Como las entalpías de formación se estandarizan para un mol de compuesto formado, debemos multiplicar dichas entalpías de formación por los coeficientes estequiométricos correspondientes de cada compuesto:

Y como:

Y, de forma general, se puede expresar del siguiente modo:

Que es la fórmula que emplearemos, en general, para el cálculo de la energía de una reacción química a partir de los valores de entalpía de formación de los reactivos y de los productos.

En el vídeo explicaremos, asimismo, cómo aplicar dicha fórmula a la reacción de combustión del benceno, es decir:

Del mismo modo, cabe destacar que con esta fórmula es posible calcular la entalpía de formación de un compuesto conociendo la entalpía de la reacción y la entalpía de formación de los compuestos restantes; esto se verá con mayor detenimiento en los ejercicios de termoquímica resueltos.

A continuación se muestra una tabla con los valores de entalpías estándar de formación (a 25ºC y 1 atm). Se puede descargar como imagen clicando sobre ella, o en PDF en el enlace inferior.

Tabla de valores de entalpías de formación estándar de diversos compuestos en PDF

Cuando se forma un enlace químico estable se desprende una cierta cantidad de energía, que será la misma cantidad de energía que se debe aportar posteriormente para romper el enlace formado. A esta energía se la denomina entalpía de enlace (si tiene lugar a presión constante) o, más coloquialmente, energía de enlace. Así, podemos definir la entalpía de enlace normal o estándar como la variación de entalpía o calor liberado, en condiciones estándar de 1 atmósfera y 25ºC, que acompaña a la reacción de formación de un mol de enlaces a partir de los átomos aislados en estado gaseoso. Como cuando se forma un mol de enlaces se desprende energía, la entalpía de enlace de este proceso será negativa:

Si en lugar de considerar la reacción de formación de un mol de enlaces consideramos la reacción inversa, es decir, la disociación de un mol de Cl2, la entalpía de dicha reacción tendrá la misma magnitud pero signo contrario:

Cuanto mayor es el valor absoluto de energía de enlace, mayor es la fortaleza de dicho enlace. Por ejemplo, para la reacción de formación de un mol de H2 a partir de los átomos de H en estado gaseoso:

Como la entalpía o energía de enlace es mayor para la molécula de H2 que para la molécula de Cl2, significa que el enlace H-H es más fuerte que el enlace Cl-Cl.

El valor de la energía de enlace puede determinarse de forma precisa para moléculas diatómicas, como las del ejemplo, y también O2, N2, F2… y para moléculas poliatómicas que tengan todos los enlaces iguales, como H2O, NH3 o CH4. Pero cuando tenemos moléculas poliatómicas con enlaces de distinto tipo, determinar la energía de enlace precisa no es posible. Por ello, en verdad se toma una entalpía de enlace media y los valores que aparecen en tablas se han calculado a partir de distintas moléculas que presentan dicho enlace. Por este motivo, las entalpías de enlace tabuladas presentan un margen de error; no son precisas, y sólo se usan para realizar cálculos aproximados cuando no se dispone de otros valores experimentales precisos, como las entalpías de formación de los compuestos que intervienen en la reacción.

Además, sólo son aplicables para moléculas covalentes sencillas, no siendo aplicables para compuestos muy polares o iónicos, ya que éstas presentan fuerzas electrostáticas que afectan a las entalpías de enlace.

Vemos a continuación una tabla con los valores de entalpía de diversos enlaces. Clicando sobre ella se puede descargar en modo imagen, y también en PDF en el enlace inferior.

Tabla de entalpías o energías de enlace en PDF

A continuación tenéis otro fenómeno bastante bonito:

Aunque parece magia, la verdad es que tiene un poco de truco. Es cierto que introducen agua en los vasos pero estos, previamente, tienen unas gotitas de indicador ácido-base de distinto tipo en el fondo. Es suficiente con esto, unas gotitas, para observar el espectacular cambio de color que se produce al variar el pH de neutro (agua) a básico agregando la disolución de hidróxido sódico, NaOH. El motivo es que los indicadores ácido base son sustancias intensamente coloreadas y, de hecho, usamos en el laboratorio y también en experiencias visuales como esta dicha propiedad. Por ejemplo, seguro que alguna vez has visto una valoración ácido base de ácido clorhídrico con hidróxido sódico utilizando el indicador fenolftaleína, el cual pasa de incoloro a fucsia en cuanto el pH pasa de 10, para lo que suele bastar una gotita en exceso de hidróxido sódico.

En concreto, en esta experiencia usan una gama de indicadores de pH que tengan los colores del arcoiris al  pH básico que aporta la disolución de hidróxido sódico. Por ejemplo, pueden usar los que se muestran en la tabla siguiente con sus correspondientes intervalos de viraje:

Con estos indicadores o también con distintas combinaciones de ellos, se puede lograr el bonito y espectacular efecto del arcoiris químico.

Al final del vídeo, cuando la totalidad del líquido vuelve a ser incoloro, es porque se ha vuelto a disminuir el pH básico que provocaba los colores, por lo que dentro del recipiente grande tiene que haber contenido un ácido como puede ser el clorhídrico.

¿Qué os parece? ¿Bonito? Pues ya sabéis, es una experiencia ideal para realizar a vuestros alumnos en clase o, si sois alumnos, para realizar a vuestros compañeros en alguna clase o feria de la ciencia.

Una reacción química consiste en el reagrupamiento o reordenamiento de los átomos de los reactivos para formar los productos. Así, algunos enlaces de los reactivos se rompen y se forman enlaces nuevos para dar las moléculas de los productos. Conociendo qué enlaces se rompen y qué enlaces se forman durante una reacción, es posible calcular su entalpía de reacción a partir de las energías de dichos enlaces. Ahora bien, los valores de entalpía de enlace son valores medios e imprecisos, y por este motivo sólo se usan para calcular entalpías de reacción de forma aproximada, cuando no se dispone de valores experimentales de entalpías de formación. En todo caso, son más fiables las entalpías de reacción calculadas a partir de las entalpías de formación que de las entalpías de enlace.

La fórmula empleada para calcular la enltapía de reacción con las energías de enlaces rotos y enlaces formados es:

Para considerar la energía de los enlaces rotos, hay que tener en cuenta la entalpía de cada tipo de enlace y multiplicar la misma por el número de enlaces que se rompen dentro de una molécula y por el coeficiente estequiométrico de la molécula de la cual proceden.

Veamos un ejemplo muy sencillo de cálculo de la entalpía de reacción para el cloruro de hidrógeno, HCl:

Como este valor obtenido es para la formación de 2 moles de HCl, para 1 mol de HCl la entalpía será la mitad, -90 kJ/mol.

En este apartado vamos a ver una tercera forma de calcular la entalpía de una reacción química, que es por aplicación directa de la Ley de Hess, ley anunciada en 1840 por el químico suizo German Henry Hess. Esta Ley también puede llamarse Ley de aditividad de las entalpías de reacción. Se trata de un método útil cuando no es posible calcular las entalpías de reacción a partir de las entalpías de formación, o en reacciones en las que la entalpía de reacción no se puede determinar experimentalmente por ser ésta muy lenta o muy explosiva.

Para llegar al fundamento de la Ley de Hess, vamos a considerar un ejemplo antes de enunciarla. Se trata de la reacción de formación de CO2(g):

Esta reacción se puede producir tal y como la hemos escrito, en una sola etapa, o también puede darse en dos etapas. En una primera etapa se formaría monóxido de carbono, CO, y después, una vez formado el monóxido de carbono, éste vuelve a reaccionar con oxígeno para dar CO2. Las etapas son:

La energía total desprendida en la formación de 1 mol de CO2 es la misma tanto si se da en una etapa como en dos, ya que para determinar la energía total desprendida cuando se da en dos etapas basta sumar las variaciones de entalpía de las etapas en las que transcurre.

ΔH1 = ΔH2 + ΔH3

-393,5 = -110,4 + (-283,1)

Esta es la base de la Ley de Hess, que la variación de entalpía asociada a una reacción química efectuada a presión constante, es la misma si se verifica directamente en una sola etapa o en varias. De forma general:

Otra forma de enunciar la Ley de Hess es:

Cuando una reacción química puede expresarse como suma algebraica de otras reacciones, su entalpía de reacción es igual a la suma de las entalpías de las reacciones parciales.

La Ley de Hess permite tratar las ecuaciones termoquímicas como ecuaciones algebraicas, y pueden sumarse, restarse o multiplicarse por un número, igual que las entalpías de reacción, para hallar la ecuación termoquímica deseada.

En el vídeo veremos, asimismo, un ejemplo sencillo de aplicación de la Ley de Hess para el cálculo de la entalpía de una reacción química.

En el tema de Enlace Químico, concretamente al calcular la energía reticular de un compuesto iónico mediante el Ciclo de Born-Haber, hemos visto algunas variaciones de entalpía referidas a cambios físicos, como la entalpía de vaporización o la entalpía de sublimación. Vamos a ver en este apartado a qué hacen referencia estas entalpías.

Supongamos que tenemos 1 mol de agua a 20ºC. Este mol de agua tendrá una entalpía inicial H1, cuyo valor absoluto no podemos conocer porque sólo podemos calcular variaciones. Si este mol de agua lo calentamos hasta 50ºC a presión constante, harán falta aportar 2257 J en forma de energía calorífica. Como la entalpía es transferencia de calor a presión constante, la entalpía de este mol de agua habrá aumentado 2257 J, es decir, la ΔH será de 2257 J.

Si durante este calentamiento del agua llegamos a los 100ºC, entonces alcanzaremos el punto de ebullición del agua, y la temperatura permanecerá constante mientras se produce el cambio de fase de líquido a vapor; es decir, mientras se produce el cambio de estado. Que la temperatura permanezca constante durante el cambio de estado no implica que no estemos aportando calor al sistema, sino que este calor se está empleando en romper las fuerzas intermoleculares del agua líquida, los enlaces de hidrógeno entre las distintas moléculas de agua, para que pasen a estado vapor y no para aumentar la temperatura del agua. A este calor necesario a presión constante para romper todos los enlaces de hidrógeno del agua líquida se le llama Entalpía de vaporización o Calor de vaporización. En el agua se necesitan 40,7 kJ/mol de energía calorífica para que un mol de agua líquida a 100ºC pase a 1 mol de agua vapor a 100ºC (Nótese la gran cantidad de energía calorífica que se necesita para hervir el agua, 40700 J/mol, cuando para calentar esa misma cantidad de agua 30ºC, de 20ºC a 50ºC, bastan sólo, como hemos comentado, 2257 J, 18 veces menos).

Si lo que tenemos es el proceso contrario, es decir, la condensación de 1 mol de agua vapor a 100ºC para dar 1 mol de agua líquida a la misma temperatura, se desprenden -40,7 kJ/mol.

Es decir, las entalpías de vaporización y condensación de una sustancia tienen la misma magnitud pero signo contrario.

ΔHvap = -ΔHcond

Del mismo modo, cuando pasamos de un mol de sustancia sólida a un mol de sustancia líquida, al alcanzar el punto de fusión de dicha sustancia, el calor necesario para romper las interacciones que mantienen unido el sólido es el llamado Calor de fusión o entalpía de fusión SÍMBOLO, que, en el caso del agua, es de 6,02 kJ/mol. La entalpía de fusión es igual pero de signo contrario que la entalpía de solidificación.

ΔHfus = -ΔHsolid

Asimismo, algunas sustancias, como el yodo, pasan directamente de sólido a vapor sin pasar por el estado líquido. Al calor necesario para esto a presión constante se le denomina Entalpía de sublimación.

A continuación hallamos una tabla con las entalpías de cambio de estado de algunas sustancias juntamente con sus puntos de fusión y de ebullición.

En este primer ejercicio resuelto de termodinámica vamos a calcular la variación de energía interna de un gas que se halla encerrado dentro de un cilindro que dispone de un pistón móvil de cierto peso. Asimismo, también nos dan el valor del calor, Q, absorbido por el gas. De este modo, aplicaremos la fórmula relativa al trabajo de expansión o compresión de un gas y la expresión del Primer Principio de la Termodinámica:

El enunciado completo es:

Se dispone de un cilindro que contiene un gas y está dotado de un pistón de 5kN de peso. Se calienta el gas y el pistón se desplaza 40 cm. Considerando que el calor absorbido por el gas es de 60 J, calcular la variación de energía interna.

El esquema para este cilindro será:

También te puede interesar:

Trabajo de expansión y compresión de un gas