En este ejercicio vamos a determinar qué tipo de hibridación presentan los átomos de una molécula orgánica (a excepción de los hidrógenos, que evidentemente no presentan ningún tipo de hibridación porque únicamente disponen de un electrón en el orbital 1s). Para ello debemos observar el número de electrones que tendrá cada átomo en la capa de valencia (3 en el caso del boro, 4 en el caso del carbono) y de qué modo se han de distribuir o desaparear estos electrones para formar el número de enlaces observados. Asimismo, la presencia de dobles o triples enlaces en las uniones carbono-carbono nos indicará también el tipo de hibridación:

• Carbono que forma 4 enlaces simples: hibridación sp3, tetraédrica
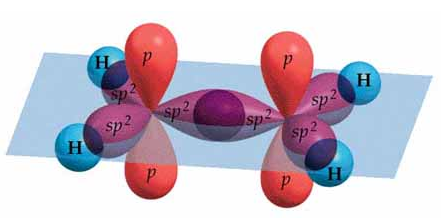
• Carbono que forma 2 enlaces simples y 1 enlace doble: hibridación sp2, trigonal plana
• Carbono que forma 1 enlace simple y 1 enlace triple, o 2 enlaces dobles: hibridación sp, lineal

El enunciado completo es el siguiente:

Indicar el tipo de hibridación de los átomos de la molécula siguiente, sabiendo que el número atómico del carbono es 6 y el del boro 5:

En este ejercicio de enlace químico vamos a determinar la estructura de Lewis de la molécula de fosgeno, COCl2, así como la hibridación que presenta el átomo central y a estudiar algunos parámetros de enlace, como por ejemplo la distancia de enlace y el ángulo.

El enunciado es:

El fosgeno, COCl2, es un gas tóxico usado en múltiples aplicaciones industriales, que también se usó como arma química en la Primera Guerra Mundial. ¿Qué hibridación presentará el átomo central y qué geometría? ¿Serán las distancias y ángulos de enlace iguales en todos los casos?

En el caso de las distancias de enlace, serán distintas porque un enlace doble será más corto, en general, que un enlace simple. Además, el oxígeno es un átomo menos voluminoso que el cloro, por lo que incluso el enlace simple C-O será más corto que el enlace C-Cl, cuando más el doble enlace C=O.

En cuanto a los ángulos de enlace, la densidad electrónica del doble enlace C=O es mayor que la de los enlaces C-Cl, esto hará que ejerza una mayor repulsión este enlace sobre los vecinos, por lo que dichos enlaces C-Cl se cerrarán más y este ángulo, en lugar de los 120º esperables por la hibridación sp2 del carbono y la geometría plana trigonal, es de 112º.

También te puede interesar:

Determinar la geometría de algunas moléculas por RPECV e hibridación

Determinar el tipo de hibridación de los átomos de una molécula orgánica

En este ejercicio de enlace químico nos piden determinar la estructura de Lewis de los iones oxonio, H3O+, y del ion amonio, NH4+, así como indicar la hibridación del átomo central en cada uno de ellos y la geometría esperable.

Estructura de Lewis del ión hidronio u oxonio, H3O+

Estructura de Lewis del ión amonio, NH4+

Puesto que ambos iones presentan un átomo central rodeado por 4 pares electrónicos, la disposición de dichos pares será tetraédrica, y la hibridación tanto del oxígeno en el ion oxonio como del nitrógeno en el ion amonio, será hibridación tetraédrica o sp3. No obstante, puesto que el ion oxonio presenta un par de electrones libre, su geometría final no será tetraédrica, ya que el par de electrones no enlazantes no se tiene en cuenta para determinar la geometría. Así, el ión oxonio tendrá geometría de pirámide trigonal, mientras que el ion amonio tendrá geometría tetraédrica (los cuatro pares son enlazantes).

También puede interesarte:

Enlace covalente coordinado o dativo

En este ejercicio determinaremos el tipo de enlace, la geometría, la hibridación y el ángulo de enlace esperado para la molécula de difluoruro de oxígeno, F2O. El enunciado es el siguiente:

“El flúor (Z = 9) y el oxígeno (Z = 8) pueden reaccionar entre ellos en determinadas condiciones para dar el difluoruro de oxígeno. Razonar el tipo de enlace que se dará entre ellos, la geometría de la molécula, el valor esperado del ángulo de enlace y la polaridad global.”

Puesto que la diferencia de electronegatividad entre el flúor (EN= 4,0) y el oxígeno (EN= 3,5) es pequeña, se tratará de un enlace covalente (recordemos que según la fórmula empírica determinada por Linus Pauling, un enlace tendrá más de un 50% de carácter covalente cuando su diferencia de electronegatividades sea menor de 1,7). Asimismo, veremos en la explicación cómo determinar su estructura de Lewis, que será:

Como el oxígeno será el átomo central y tendrá en torno a él 4 pares electrónicos (2 enlazantes y 2 no enlazantes) estos pares se distribuirán de forma tetraédrica (hibridación sp3), pero no se tendrán en cuenta a la hora de determinar la geometría, por lo que se tratará de una geometría angular. En cuanto al ángulo de enlace, aunque para un tetraedro sabemos que es de 109º, habrá variación del mismo por el hecho de que el oxígeno presente pares libres. Los pares libres ejercen una mayor repulsión que los enlazantes F-O, y por tanto estos se aproximarán mutuamente, dando lugar a un ángulo de enlace inferior al de 109º.

La molécula será levemente polar ya que, aunque la diferencia de electronegatividad es pequeña, la geometría angular hará que unas de las componentes de los momentos dipolares se sumen, dando lugar a un momento dipolar total distinto de cero.

También te puede interesar:

Determinar le estructura de Lewis, la geometría por RPECV y la hibridación de CS2, CHCl3, OCl2 y PH3

Determinar la estructura de Lewis, la hibridación, la geometría y los parámetros de enlace del fosgeno, COCl2

Determinar la estructura de Lewis, la hibridación y la geometría de los iones oxonio y amonio

En este ejercicio vamos a determinar la polaridad de algunos enlaces de una molécula orgánica, la 3-cloro-2-butanona, además de formular el compuesto, y también la densidad de carga de cada uno de los átomos implicados en el enlace. El enunciado completo es:

“Formular la molécula de 3-cloro-2-butanona e indicar los enlaces polarizados que posee, especificando la densidad de carga de cada átomo del enlace (δ-, δ+).”

La estructura de Lewis para esta molécula es la siguiente:

Recordemos que la densidad de carga negativa de un enlace polarizado corresponde al átomo más electronegativo, porque es éste el que atrae más hacia sí la nube electrónica, quedando en parte con un exceso de carga negativa o de electrones, y por tanto como δ-.

En este ejercicio de enlace químico vamos a formular el compuesto 2-cloropropeno y vamos a determinar cuáles son los enlaces polarizados que presenta. El enunciado completo es:

“Escribir la fórmula química del 2-cloropropeno, indicando los enlaces polarizados con la densidad de carga de cada átomo, y un enlace pi. ¿Qué enlace, σ o π, requiere más energía para ser disociado? ¿Por qué?”

En este sentido, como veremos en la explicación en profundidad, el enlace σ C-C es más fuerte y requiere más energía para su disociación que el enlace π C-C porque el solapamiento frontal hace que sea mayor la interpenetración de los orbitales y, por tanto, más difíciles de separar que el π, donde los orbitales p solapan lateralmente.

En este ejercicio de enlace químico vamos a resolver una cuestión más teórica sobre los distintos enlaces carbono-carbono, es decir, el enlace simple, con hibridación sp3, y los enlaces múltiples, con hibridación sp (un carbono con triple enlace o con dos dobles enlaces) o hibridación sp2 (un carbono con un doble enlace).

El enunciado completo es:

“Los enlaces dobles y triples carbono-carbono son rígidos, sin capacidad de giro, mientras que los enlaces simples carbono-carbono pueden rotar sobre sí mismos con cierta libertad (la rotación requiere un aporte energético pequeño). Justificar este hecho en base al solapamiento orbital”.

Como veremos en el vídeo con mayor detenimiento, la justificación es la siguiente:

• El enlace simple C-C es un enlace de solapamiento frontal de tipo σ, entre un orbital híbrido sp3 y otro orbital híbrido sp3. El hecho de que el solapamiento sea frontal hace que pueda rotar fácilmente:

• Los enlaces dobles y triples presentan respectivamente, además del enlace simple de tipo σ, uno y dos enlaces de tipo π. Estos enlaces π corresponden al solapamiento lateral de dos orbitales p no hibridados y paralelos. Este enlace requiere que los dos orbitales estén así, estrictamente paralelos entre sí, por lo que la rotación del enlace implica necesariamente su ruptura.

En este ejercicio de enlace químico explicaremos por qué el sodio (un metal alcalino) y el berilio (un metal alcalinotérreo) son buenos conductores eléctricos en base a la teoría de bandas. El enunciado completo es:

“En base a la teoría de bandas, explicar la conductividad eléctrica del sodio. ¿Por qué el berilio, que tiene el orbital 2s completo, es un buen conductor de la electricidad?”

Recordemos que los orbitales atómicos de los metales forman un conjunto de orbitales moleculares que pertenecen a la totalidad de la red metálica y que, al estar muy próximos entre ellos en energía, reciben el nombre de banda, tal y como vemos a continuación:

Esta banda se forma tanto con los orbitales atómicos de valencia, dando lugar a la llamada banda de valencia, como con los sucesivos orbitales vacíos o semillenos (normalmente orbitales p), dando lugar a la llamada banda de conducción. Cuando las bandas de valencia y de conducción solapan, estamos ante un elemento conductor de la corriente eléctrica, porque los electrones tienen cierta libertad para promocionar de una banda a otra:

También te puede interesar:

Teoría de bandas para explicar el enlace metálico (vídeo de teoría)

En este ejercicio de enlace químico de carácter tal vez más teórico que el resto, vamos a resolver algunas cuestiones de verdadero o falso sobre el enlace metálico y las propiedades de los elementos metálicos. El enunciado completo es:

Razonar si son ciertas o falsas las siguientes afirmaciones referentes a los metales:

a) La red cristalina de los metales está formada por iones positivos y negativos.

b) Los electrones de valencia de los metales están situados en orbitales deslocalizados.

c) La red cristalina de los metales está formada sólo por iones positivos.

d) La dureza de los metales y sus puntos de fusión relativamente elevados se explican suponiendo que los átomos metálicos se encuentran unidos por enlaces covalentes.

e) Algunos metales sólidos son amorfos.

Tal vez también te interese:

Modelo del mar de electrones para el enlace metálico

Teoría de bandas para el enlace metálico

Propiedades de los elementos metálicos

En este ejercicio vamos a determinar la energía reticular desprendida cuando se forma un mol de compuesto AB a partir de sus iones A(2+) y B(2-) en estado gaseoso, a partir de la ecuación de Born-Landé. El enunciado completo es:

Calcular la energía reticular de un compuesto AB, de iones divalentes, sabiendo que la distancia interiónica es de 2,59A; la constante de Madelung, 1,7476, y el coeficiente de Born, 9.

En este ejercicio será muy importante tener en cuenta las unidades en las que se deben poner todos los parámetros indicados en la ecuación de Born-Landé, por lo que incluiremos en la ecuación expresada a continuación, la constante de Coulomb, k.

En este ejercicio de enlace químico vamos a aplicar de forma cualitativa la ecuación de Born-Landé para determinar cuál de dos compuestos iónicos presentará una mayor dureza. El enunciado es el siguiente:

“¿Qué compuesto tendrá mayor dureza, el KBr o el NaBr?”

Para ello debemos recordar que cuanto mayor sea la energía reticular de un compuesto iónico, mayor será la dureza del mismo. Asimismo, la energía reticular es inversamente proporcional a la distancia interiónica (cuanto mayor sea la distancia menor será la energía reticular) mientras que es directamente proporcional a la carga de los iones. En este caso concreto, al ser la carga de los iones la misma (cationes K+ y Na+, anión Br-) el factor diferencial entre el bromuro potásico, KBr, y el bromuro sódico, NaBr, es la distancia interiónica. Puesto que el catión potasio tiene un radio mayor que el catión sodio, la distancia interiónica del KBr será mayor y, por tanto, menor su energía reticular. Si el KBr tiene una menor energía reticular, éste será el compuesto de menor dureza y el NaBr el de mayor dureza.

En este ejercicio de enlace químico vamos a determinar cómo afectan distintas variaciones en la carga o en el tamaño de los iones que forman un compuesto iónico genérico AB. Así, se trata de determinar en qué medida aumenta o disminuye la energía reticular del compuesto iónico a partir de la ecuación de Born-Landé, sabiendo que dicha energía reticular es directamente proporcional al producto de cargas e inversamente proporcional a la distancia interiónica, es decir:

El enunciado completo es:

Determinar cómo afectarán las siguientes variaciones a la energía reticular de una red cristalina formada por A+,B-:

a) Duplicar el radio de A+ y de B-

b) Duplicar la carga de A+

c) Duplicar las cargas de A+ y B-

d) Disminuir a la mitad los radios de A+ y B-

En este ejercicio determinaremos, de un grupo de compuestos iónicos, cuál tendrá mayor energía reticular y cuál tendrá mayor punto de fusión, a partir de la relación cualitativa que establece la ecuación de Born-Landé; recordemos que la energía reticular es directamente proporcional al producto de cargas de los iones, e inversamente proporcional a la distancia interiónica.

Cabe tener en cuenta, además, que la relación entre el punto de fusión y la energía reticular es directamente proporcional, es decir, cuanto mayor es la energía reticular de un compuesto, mayor es su punto de fusión, ya que debemos aportar mayor cantidad de energía para lograr separar los iones entre sí (si la energía reticular del compuesto en valor absoluto es muy grande, significa que los iones están unidos muy fuertemente). Por tanto, los compuestos con menor punto de fusión, que es lo que nos piden en el apartado b del ejercicio, serán aquellos que tengan una menor energía reticular.

Los dos grupos de compuestos iónicos que vamos a comparar difieren o bien en el catión (NaF, fluoruro sódico, KF, fluoruro potásico, LiF, fluoruro de litio) o bien en el anión (NaF, fluoruro sódico, NaCl, cloruro sódico, NaBr, bromuro sódico). De esta forma, puesto que las cargas iónicas no cambian, el único elemento diferencial será la distancia interiónica; presentarán menor energía reticular los compuestos con radios iónicos mayores, puesto que si los iones están más alejados (son de mayor tamaño) cuesta menos separarlos.

El enunciado completo es:

Supongamos que los sólidos cristalinos siguientes, en cada uno de los grupos, cristalizan en el mismo tipo de red: grupo 1 , NaF, KF, LiF, grupo 2, NaF, NaCl, NaBr. Razona tus respuestas:

a) Los compuestos con más energía de red de cada grupo.

b) Los compuestos con menor punto de fusión en cada grupo.

También te puede interesar:

TEORÍA DE LA ECUACIÓN DE BORN-LANDÉ PARA LA ENERGÍA RETICULAR

Energía reticular a partir de la ecuación de Born-Landé

EJERCICIOS DE LA ECUACIÓN DE BORN-LANDÉ PARA LA ENERGÍA RETICULAR

Cálculo directo de la energía reticular de un compuesto iónico AB por la ecuación de Born-Landé

Comparación de la dureza de dos compuestos iónicos, NaBr y KBr, por la ecuación de Born-Landé

Determinar cómo afectan variaciones de los iones A y B a la energía reticular de AB con Born-Landé

En las últimas semanas hemos tenido el blog quizá un tanto abandonado. Aunque ya estoy preparando algunas entradas que me parecen muy interesantes, relacionadas con la Primera Guerra Mundial (ya sabéis que me encanta la relación entre la Química y la historia) y con los últimos descubrimientos del Curiosity, se trata de entradas que me van a llevar bastante trabajo en cuanto a documentación y elaboración, porque cuanto más indago, más detalles extraordinarios descubro que no quiero dejar de comentar. Así que para estas habrá que esperar un poco, y he querido escribir otra entrada previa para dar señales de vida y gritar: “¡La inspiración nos ha pillado trabajando!”.

El motivo de tener el blog menos actualizado de lo habitual es que estamos en plena “fiebre” de contenidos. En las últimas semanas hemos grabado ya 34 vídeos de ejercicios resueltos de enlace químico y hemos procesado y anexado gran parte de ellos, que podéis ver en el enlace. No son estos 34 la totalidad de ejercicios del tema, que ascenderán a la friolera de 47 ejercicios resueltos (los 13 restantes ya están a punto de grabar). Como veis, Enlace Químico es un tema denso y complejo, y por este motivo es de los que más ejercicios abarca, tanto en cuanto a tipos como a variedad: ejercicios genéricos de determinación del tipo de enlace, estructuras de Lewis, geometría e hibridación de moléculas covalentes, enlace metálico, enlace iónico, fuerzas intermoleculares, propiedades de los compuestos… Hemos querido recopilar en estos 47 ejercicios que hemos seleccionado con sumo cuidado todos estos aspectos y también profundizar en ellos, mostrando diferentes niveles de dificultad. Pronto, en cuanto los tengamos todos, subiremos también el pdf correspondiente con todos los enunciados para que podáis evaluar cuáles de estos ejercicios resueltos os serán más provechosos para vuestro estudio.

Por si esto fuera poco, en cuanto acabemos de grabar los 13 ejercicios de enlace químico que aún están en el tintero, empezaremos con Termoquímica. Como siempre empezaremos por la teoría: documentación, organización de los contenidos, decidir cómo y en qué orden tratarlos, en qué profundidad, cómo explicarlo de la forma más sencilla posible… Si habéis visto con frecuencia nuestros materiales sabréis que no siguen un libro al pie de la letra, sino que los elaboramos para que sean comprensibles y que sigan un orden creciente de dificultad. Por esto no será un material que tengamos elaborado de forma inmediata, lleva su tiempo, pero las recompensas, que son vuestro aprendizaje y vuestros buenos resultados, merecen la pena.

Aquí seguimos, ¡quemando gasolina!

En este ejercicio de enlace químico vamos a ordenar de mayor a menor energía reticular cuatro compuestos iónicos que difieren en sus cationes y en sus aniones. Son: sulfuro de calcio, CaS, óxido de calcio, CaO, yoduro potásico, KI, y fluoruro potásico, KF.

Para poder realizar esta ordenación debemos recordar la relación existente entre la energía reticular de un compuesto iónico y dos parámetros: por una parte, las cargas de los iones que forman la red cristalina, Z1 y Z2 y, por otra, la distancia interiónica. Así, cuanto mayor es el producto de cargas de los iones, mayor es la energía reticular (directamente proporcional) mientras que cuanto mayor es el tamaño de los iones menor es la energía reticular (inversamente proporcional). Esto hará que los compuestos de calcio tengan una energía reticular muy superior a los compuestos de potasio, ya que en el CaS y en el CaO, el producto de cargas es 4, mientras que en KI y KF, el producto de cargas es 1.

TEORÍA DE LA ECUACIÓN DE BORN-LANDÉ PARA LA ENERGÍA RETICULAR

Energía reticular a partir de la ecuación de Born-Landé

EJERCICIOS DE LA ECUACIÓN DE BORN-LANDÉ PARA LA ENERGÍA RETICULAR

Cálculo directo de la energía reticular de un compuesto iónico AB por la ecuación de Born-Landé

Comparación de la dureza de dos compuestos iónicos, NaBr y KBr, por la ecuación de Born-Landé

Determinar cómo afectan variaciones de los iones A y B a la energía reticular de AB con Born-Landé

Energía reticular y punto de fusión de NaF, KF, LiF y NaF, NaCl, NaBr

En este ejercicio 27 de enlace químico, vamos a responder algunas cuestiones acerca del Ciclo de Born-Haber para el compuesto iónico formado por flúor y sodio, es decir, el fluoruro sódico, NaF. El enunciado completo es:

A partir del esquema del Ciclo de Born-Haber para el fluoruro de sodio:

a) Indique el nombre de las energías implicadas en los distintos procesos.

b) Justificar si son negativas o positivas las energías implicadas en los procesos 1,2, 3, 4 y 5.

c) En función del tamaño de los iones, justifique si la energía reticular del fluoruro de sodio es mayor o menor, en valor absoluto, que la del cloruro sódico. 

En este ejercicio determinaremos la energía reticular del fluoruro cálcico, CaF2, tanto a partir del ciclo de Born-Haber como de la ecuación de Born-Landé, comparando ambos valores.

El enunciado completo es:

A partir de los datos expuestos, calcular la energía reticular del fluoruro cálcico a partir del ciclo de Born-Haber y de la ecuación de Born-Landé.

ΔHsub (Ca) = 193 kJ/mol

(entalpía de sublimación del calcio, es decir, energía necesaria para pasar el calcio de sólido a vapor).

EI1 (Ca) = 540 kJ/mol

(primera energía de ionización del calcio, es decir, energía necesaria para abstraer un electrón de valencia del calcio gaseoso, quedando el catión Ca+ también en estado gaseoso).

EI2 (Ca) = 1150 kJ/mol

(segunda energía de ionización del calcio, es decir, energía necesaria para abstraer el segundo electrón de valencia del catión Ca+, quedando como catión Ca2+, en estado gaseoso).

ΔHdis (F2) = 158 kJ/mol

(entalpía de disociación del flúor, energía necesaria para disociar la molécula diatómica F2 a átomos individuales, F(g)).

AE (F) = -333 kJ/mol

(afinidad electrónica del flúor, energía desprendida cuando un átomo de flúor capta un electrón para quedar como anión fluoruro, F-).

ΔHf (CaF2) = -1214,6 kJ/mol

(entalpía de formación del fluoruro de calcio, energía desprendida cuando se forma un mol del compuesto sólido a partir de sus elementos en estado natural, es decir, calcio metálico sólido y flúor diatómico y gaseoso).

Distancia interiónica = 2,35 Å

Cte de Madelung = 2,5194

Coef. Born o factor de compresibilidad = 8

K (constante de Coulomb) = 9·10^9 N·m2/C2

e = 1,60·10^(-19) C

El ciclo de Born-Haber para este compuesto se representa del siguiente modo:

Tal vez también te interese:

Ciclo de Born-Haber para el fluoruro sódico, NaF

Ordenar de mayor a menor energía reticular KI, CaS, KF y CaO

Energía reticular y punto de fusión de NaF, KF, LiF y NaF, NaCl, NaBr

Comparación de la dureza de dos compuestos iónicos por la ecuación Born-Landé

En el siguiente ejercicio calcularemos la energía reticular del bromuro potásico, KBr, a partir del ciclo de Born-Haber, utilizando para ello los datos siguientes:

ΔHf (KBr) = -391,8 kJ/mol

(entalpía de formación del bromuro potásico, energía desprendida cuando se forma un mol de bromuro potásico a partir de sus elementos en estado natural, es decir, potasio sólido metálico y bromo diatómico líquido)

ΔHvap (Br2) = 30,7 kJ/mol

(entalpía de vaporización del bromo, es decir, energía necesaria para pasar de líquido a vapor).

ΔHdis (Br2) = 193,5 kJ/mol

(entalpía de disociación del bromo, es decir, energía necesaria para pasar de molécula diatómica gaseosa a átomos individuales gaseosos, Br2(g) –> 2Br(g)).

ΔHsub (K) = 81,3 kJ/mol

(entalpía de sublimación del potasio, energía necesaria para pasar de potasio sólido a potasio gaseoso).

EI (K) = 418,4 kJ/mol

(energía de ionización del potasio, energía necesaria para ionizar el potasio, abstrayendo el electrón de valencia y pasando a catión potasio, K+).

AE Br = -321,9 kJ/mol

(afinidad electrónica del bromo, energía desprendida cuando un átomo de bromo en estado gaseoso capta un electrón para pasar a anión bromuro, Br-).

También te pueden interesar los ejercicios siguientes:

Ciclo de Born-Haber para el fluoruro sódico, NaF

Cálculo de la energía reticular del fluoruro cálcico, CaF2, por el Ciclo de Born-Haber y la ecuación de Born-Landé

En este ejercicio vamos a determinar la energía reticular del óxido de magnesio, MgO. La diferencia con respecto a los ejercicios del Ciclo de Born-Haber realizados previamente se halla en el hecho de que el anión oxígeno presenta una carga neta de -2, por lo que debemos considerar dos valores de afinidad electrónica, un primer valor para pasar de O(g) a O(-)(g), y un segundo valor para pasar de O(-)(g) a O(-2)(g). Del mismo modo, para el magnesio debemos considerar dos valores de energía de ionización, un primer valor para pasar de Mg(g) a Mg(+)(g), y un segundo valor para pasar de Mg(+)(g) a Mg(2+)(g), tal y como se puede apreciar en el esquema del ciclo de Born-Haber.

Los datos de que disponemos para realizar el cálculo de la energía reticular del óxido de magnesio son:

ΔHf (MgO) = -602,0 kJ/mol

(entalpía de formación del óxido de magnesio, energía desprendida cuando se forma un mol del compuesto sólido a partir de sus elementos en estado natural, es decir, magnesio metálico, sólido, y oxígeno como gas diatómico).

ΔHsub (Mg) = 146,1 kJ/mol

(entalpía de sublimación del magnesio, es decir, energía necesaria para que el magnesio metálico en estado sólido pase a magnesio vapor).

ΔHdis (O2) = 498,2 kJ/mol

(entalpía de disociación del oxígeno, energía necesaria para pasar de oxígeno diatómico gaseoso a átomos individuales de oxígeno en estado gaseoso).

EI1 (Mg) = 736,3 kJ/mol

(primera energía de ionización del magnesio, energía necesaria para abstraer un primer electrón de valencia y pasar de Mg(g) a Mg(+)(g)).

EI2 Mg = 1447,9 kJ/mol

(segunda energía de ionización del magnesio, energía necesaria para abstraer el segundo electrón de valencia y pasar de Mg(+)(g) a Mg(2+)(g)).

AE1 (O) = -141,2 kJ/mol

(primera afinidad electrónica del oxígeno, energía necesaria para pasar de O(g) a O(-)(g)).

AE2 (O) = -791,0 kJ/mol

(segunda afinidad electrónica del oxígeno, energía necesaria para pasar de O(-)(g) a O(2-)(g)).

En este ejercicio determinaremos la afinidad electrónica del cloro a partir del Ciclo de Born-Haber. Si bien es habitual en los distintos ejercicios de enlace químico usar dicho ciclo para calcular la energía reticular, en realidad podemos calcular cualquiera de los restantes parámetros implicados siempre y cuando dispongamos del resto de datos. En este caso, se trata del uso del ciclo de Born-Haber para el cloruro sódico.

El enunciado completo es:

Calcular la afinidad electrónica del cloro con los datos que se muestran a continuación:

Ur (NaCl) = -769,0 kJ/mol

(energía reticular del cloruro sódico, energía desprendida cuando se forma un mol del compuesto a partir de sus iones en estado gaseoso)

EI (Na) = 493,7 kJ/mol

(energía de ionización del sodio, energía necesaria para abstraer el electrón de valencia y formar el catión sodio, Na(+)).

ΔHf NaCl = -411,0 kJ/mol

(entalpía de formación del cloruro sódico, energía desprendida cuando se forma un mol del compuesto a partir de sus elementos en estado natural, es decir, el sodio metálico y el cloro gaseoso diatómico).

ΔH dis Cl2 = 242,6 kJ/mol

(entalpía de disociación del cloro, energía necesaria para romper en enlace Cl-Cl de un mol de moléculas y dar lugar a átomos de cloro individuales).

ΔH sub Na = 107,5 kJ/mol

(entalpía de sublimación del sodio, energía necesaria para pasar de sodio en estado sólido a sodio en estado gaseoso).

Tal vez también te interese:

Ciclo de Born-Haber para el fluoruro sódico, NaF

Cálculo de la energía reticular del fluoruro de calcio, CaF2 por Born-Haber y Born-Landé

Cálculo de la energía reticular del bromuro potásico, KBr, por el Ciclo de Born-Haber 

Cálculo de la energía reticular del óxido de magnesio, MgO, por el Ciclo de Born-Haber